Strahlungsaustausch

aus Wikipedia, der freien Enzyklopädie

Durch Strahlungsaustausch beeinflussen sich Körper im Raum gegenseitig wärmemäßig. Jeder Körper mit einer Temperatur über dem absoluten Nullpunkt sendet elektromagnetische Strahlung aus, die von anderen Körpern (und ggf. von dem Körper selbst) absorbiert wird.

Für die Temperaturverhältnisse z.B. in Wohnräumen ist der Strahlungsaustausch eine wichtige Einflußgröße. Er ist deshalb bei der Berechnung des Wärmebedarfs zu beachten. Für die rechtliche Seite ist er Bestandteil der EnEV und es wird mit standartisierten Klimabedingungen gearbeitet. Für die Auslegung der Heizanlage sind die örtlichen Klimabedingungen maßgebend.

Die Berechnung der Größe des Strahlungsaustausches ist im Allgemeinen recht kompliziert (im VDI-Wärmeatlas das Kapitel: Berechnung des Strahlungsaustauschs zwischen mehreren Oberflächen), nur für einfache Verhältnisse ist eine einfache Lösung möglich. Allerdings ist die einfache Lösung für viele Praxisfälle hinreichend genau.

Das Plancksche Strahlungsgesetz beschreibt die Ausstrahlung eines schwarzen Körpers. Das ist natürlich nur ein theoretischer Idealfall. In der Realität gibt es keine schwarzen Körper sondern nur graue Körper - die allerdings dem schwarzen Körper sehr nahe kommen können.

Auch eine zweite Vernachlässigung trifft in der Realität nie zu: kein Körper ist allein im Universum, so daß für die realen Strahlungsverhältnisse nicht nur die Ausstrahlung eines Körpers betrachtet werden darf, sondern auch die Bestrahlung durch andere Körper beachtet werden muß. Dem Idealfall keiner Bestrahlung, sondern nur Ausstrahlung kommen viele Sterne nahe, aber ideale Verhältnisse werden auch bei den Sternen nicht erreicht.

Besonders groß sind die Unterschiede zwischen den Abstraktionen zur einfachen Darstellung der physikalischen Gesetze und den realen Verhältnissen z.B. in Wohnräumen. Da haben die Wände unterschiedliche Temperaturen und Oberflächen, es sind Heizkörper vorhanden (mit weiteren Temperaturen und Oberflächen), Menschen und Tiere halten sich darin auf (mit wieder anderen Temperaturen und Oberflächen). Obwohl sich alles berechnen läßt, wird bei den vielfältigen Verhältnissen die genaue Berechnung sehr umfangreich und hat oft wenig praktischen Wert.

Beispiel für einen einfachen Strahlentausch

Oft reicht aber für die Anwendung auch wieder eine Idealisierung. Es werden zwei nebeneinander befindliche Oberflächen betrachtet. Die beiden Oberflächen sollen sehr groß gegenüber ihrem Abstand sein und zwei unterschiedliche, aber konstante Temperaturen T1 und T2 haben. Ihre Oberflächen werden durch die Angabe der Emissionskoeffizienten ε1 und ε2 beschrieben.

Aus dem einfachen Stefan-Boltzmann-Gesetz

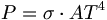
P = \sigma \cdot AT^4

wird beim Strahlungsaustausch eine temperaturabhängige Differenz

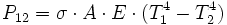
P_{12} = \sigma \cdot A \cdot E \cdot (T_1^4 - T_2^4)

In der Gleichung des Strahlungsaustauschs ist eine neue Konstante, der Strahlungsaustauschgrad E eingeführt. Für diesen Strahlenaustauschgrad E bei dem gewählten Beispiel ergibt die Rechnung:

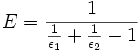
E = \frac{1}{\frac{1}{\epsilon_1} + \frac{1}{\epsilon_2} - 1}

Um die Gleichung leichter zu verstehen wird an diesem einfachen Beispiel die Berechnung des Strahlenaustauschgrads gezeigt.

Die Bedingungen werden gewählt um die Rechnung einfach zu machen.

Die erste Bedingung wird gewählt, damit die Strahlungsmenge die den Raum zwischen den beiden Platten verläßt klein ist im Vergleich zwischen der Strahlung zwischen den Platten - der Idealfall wäre, daß dieser Anteil Null ist. Die zweite Forderung wird gewählt, damit sich für die Zeit des Strahlenaustauschs und/oder der Messung die Oberflächentemperatur nicht ändert. Damit sich die Oberflächentemperatur nicht ändert, müssen den Platten die entsprechenden Leistungen extern zu- bzw. abgeführt werden, die infolge des Strahlungsaustauschs zwischen den Platten transportiert werden (analog einer Heizung mit ihrer Warmwasserzuführung für den Wärmeverlust durch die Außenwände). Ist die wärmespeichernde Masse der Oberflächen sehr groß, ist die Temperaturänderung auch ohne externe Zuführung von Leistung sehr langsam und kann ggf. vernachlässigt werden.

Außerdem darf sich zwischen den beiden Oberflächen kein weiterer Körper befinden, denn sonst wäre es ein Austausch nicht nur zwischen zwei Oberflächen, sondern zwischen noch mehr.

Unter diesen Annahmen trifft alle Strahlung, die von Oberfläche 1 emittiert wird auf die Oberfläche 2 und wird dort teilweise absorbiert und teilweise reflektiert. Die reflektierte Strahlung trifft wieder auf Oberfläche 1 und wird dort ebenfalls teilweise absorbiert und teilweise reflektiert. So geht da theoretisch bis ins Unendliche, denn erst dann ist alle emittierte Strahlung absorbiert - teils von Oberfläche 2 teils von Oberfläche 1, so daß insgesamt weniger Leistung von Oberfläche 1 abgestrahlt wird, als am Anfang der Emission, da die emittiertende Oberfläche einen Teil der emittierten Strahlung selbst absorbiert.

Zwei weitere Anmerkungen: 1. Die eben betrachteten Verhältnisse bezogen sich nur auf die Abstrahlung von Oberfläche 1, natürlich strahlt auch Oberfläche 2 und Oberfläche 1 absorbiert davon einen Teil. Die Leistung die extern den einzelnen Oberflächen zugeführt werden muß, wenn die Temperatur konstant gehalten werden soll ist natürlich die Differenz zwischen emittierter und absorbierter Leistung. 2. In der Regel sind die Emissionskoeffizienten im ganzen interessierenden Wellenlängenbereich konstant. Wenn das nicht zutrifft beschreibt die nachfolgende Strahlungsaustauschformel nur den Strahlungsaustausch bei einer bestimmten Wellenlänge. Für den Strahlungsaustausch im gesamten Wellenlängenbereich ist dann eine gewichtete Strahlungsaustauschzahl analog dem gewichteten Emissionskoeffizienten beim grauen Körper zu benutzen (die gewichtete Strahlungsaustauschzahl ist in der Regel ungleich einer (falschen) Strahlungsaustauschzahl, die sich ergibt, wenn die gewichteten Emissionskoeffizienten in die Strahlungsaustauschzahl eingesetzt würden).

Letzte Vorbemerkung:

Wo geht die Wärme hin, die von jeder der Oberflächen ausgeht? Natürlich zur anderen Oberfläche und dort wird sie teilweise absorbiert, teilweise reflektiert - eine dritte Möglichkeit gibt es bei den vorausgesetzten undurchsichtigen Flächen nicht. Wenn also eine Strahlung von einer Seite ausgestrahlt wird, wird von dieser Strahlung ein Teil r reflektiert und der Rest 1 - r absorbiert - und reale Körper haben immer Werte 0 < r < 1. Die idealen Werte 0 oder 1 gibt es in der Realität nicht. Haben beide Oberflächen die gleichen Temperaturen, so muß jede Oberfläche genau so viel absorbieren wie emittieren - wäre das nicht der Fall würde sich die Oberfläche, die mehr emittiert als absorbiert, erwärmen - die andere Oberfläche müßte sich dementsprechend abkühlen. Das widerspricht jeder Erfahrung und hätte als Konsequenz, daß ein Perpetuum mobile möglich wäre.

Aus der Tatsache, daß bei gleichen Temperaturen die absorbierte und die emittierte Wärme gleich sein muß, folgt daß ε = 1 - r oder r + ε = 1 bzw. r = 1 - ε ist.

Nach diesen Vorbemerkungen kann nun die Strahlungsaustauschzahl für das Beispiel hergeleitet werden:

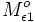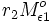Zunächst zur Strahlung, die von der Oberfläche 1 ausgeht und bei Oberfläche 2 absorbiert wird. Ausgegangen wird von der Strahlung M_{\epsilon 1}^o die von Oberfläche 1 ausgeht. Davon reflektiert Oberfläche 2 mit dem Reflexionsfaktor r2 einen Anteil r_2 M_{\epsilon 1}^o. 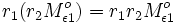Diese Strahlung fällt auf Oberfläche 1 mit dem Reflexionsfaktor r1 zurück und dementsprechend fällt nun auf die Oberfläche 2 der Anteil r_1 (r_2 M_{\epsilon 1}^o) = r_1 r_2 M_{\epsilon 1}^o. 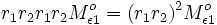Dieses Spiel wiederholt sich, so daß nach den nächsten Reflexionen die Strahlstärke r_1 r_2 r_1 r_2 M_{\epsilon 1}^o = (r_1 r_2)^2 M_{\epsilon 1}^o ist. 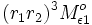Beim nächsten Mal (r_1 r_2)^3 M_{\epsilon 1}^o usw. bis ins Unendliche fortgesetzt. Um zu erhalten, wieviel Oberfläche 2 insgesamt von der einfallenden Strahlung erhalten hat sind die einzelnen absorbierten Anteile zu addieren. 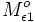Beim ersten Mal fällt M_{\epsilon 1}^o ein und der Anteil ε2 also 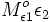M_{\epsilon 1}^o \epsilon_2 wird absorbiert. Beim zweiten Mal fällt die Leistung 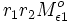r_1 r_2 M_{\epsilon 1}^o ein und wieder wird der Anteil ε2 absorbiert, also 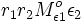r_1 r_2 M_{\epsilon 1}^o \epsilon_2 usw. Insgeamt ist also die von Oberfläche 2 absorbierten Teil der Strahlung der von der Oberfläche 1 ausgeht:

q_{a12} = M_{\epsilon 1}^o \epsilon_2 + r_1 r_2 M_{\epsilon 1}^o \epsilon_2 + (r_1 r_2)^2 M_{\epsilon 1}^o \epsilon_2 + .... = M_{\epsilon 1}^o [1 + r_1 r_2 + (r_1 r_2)^2 + ....] \epsilon_2

Der Ausdruck in der eckigen Klammer kann leicht berechnet werden, indem er zuerst als Summe S bezeichnet wird und dann wird diese Summe berechnet:

\begin{matrix} S&=&[1 + r_1 r_2 + (r_1 r_2)^2 + ....] \\ S r_1 r_2&=& r_1 r_2 [1 + r_1 r_2 + (r_1 r_2)^2 + ....]&=& [ r_1 r_2 + (r_1 r_2)^2+ (r_1 r_2)^3 + ....] \\ \end{matrix}

Nun wird die Differenz zwischen den beiden Zeilen gebildet:

\begin{matrix} S - S r_1 r_2&=&[1 + r_1 r_2 + (r_1 r_2)^2 + ....] - [ r_1 r_2 + (r_1 r_2)^2+ (r_1 r_2)^3 + ....] = 1 \\ S [1 - r_1 r_2]&=&1\\ S &=& \frac{1}{1 - r_1 r_2} \end{matrix}

Nun wird der Ausdruck (die Summenformel einer geometrischen Reihe) für S in die Gleichung für die absorbierte Strahlung eingesetzt und man erhält:

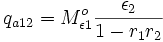
q_{a12} = M_{\epsilon 1}^o \frac{\epsilon_2}{1 - r_1 r_2}

In diese Gleichung werden die einzelnen Werte eingesetzt:

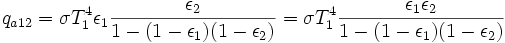
q_{a12} = \sigma T_1^4 \epsilon_1 \frac{\epsilon_2}{1 - (1 - \epsilon_1) (1 - \epsilon_2)} = \sigma T_1^4 \frac{\epsilon_1 \epsilon_2}{1 - (1 - \epsilon_1) (1 - \epsilon_2)}

Zunächst wird der Nenner ausgewertet:

1 - (1 - ε1)(1 - ε2) = 1 - (1 - ε2 - ε1 + ε1ε2) = ε2 + ε1 - ε1ε2

Wird dieser Ausdruck in die Gleichung für qa12 eingesetzt, wird:

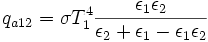
q_{a12} = \sigma T_1^4 \frac{\epsilon_1 \epsilon_2}{\epsilon_2 + \epsilon_1 - \epsilon_1 \epsilon_2}

Nun wird noch durch ε1ε2 geteilt:

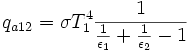
q_{a12} = \sigma T_1^4 \frac{1}{\frac{1}{\epsilon_1} + \frac{1}{\epsilon_2} - 1}

Den Rest der ursprünglich ausgesandten Strahlung hat die Oberfläche 1 selber absorbiert. Das das so ist, ist natürlich klar, man kann es aber auch mit der analogen Rechnung zeigen. Damit hat Oberfläche 1 Wärme zur Oberfläche 2 gestrahlt, die kleiner ist, als die Abstrahlung ohne Rückstrahlung gewesen wäre.

Gleichzeitig ist aber die analoge Rechnung für Oberfläche 2 und liefert den Wert für qa21. Die Bilanz der beiden Strahlungen ist für Oberfläche 1 nun ausgestrahlte Leistung minus absorbierte Leistung:

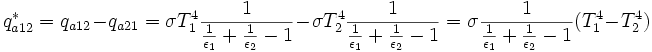
q_{a12}^* = q_{a12} - q_{a21} = \sigma T_1^4 \frac{1}{\frac{1}{\epsilon_1} + \frac{1}{\epsilon_2} - 1} - \sigma T_2^4 \frac{1}{\frac{1}{\epsilon_1} + \frac{1}{\epsilon_2} - 1} = \sigma \frac{1}{\frac{1}{\epsilon_1} + \frac{1}{\epsilon_2} - 1} (T_1^4 - T_2^4)

Anmerkung: es gibt Herleitungen dieser Formel, die die Summation einer unendlichen geometrischen Reihe benutzen, ohne das ausdrücklich zu erwähnen.

Der Teil der vorstehenden Formel, der nur die Emissionskoeffizienten enthält wird als Strahlungsaustauschgrad E (DIN EN ISO6946) bezeichnet:

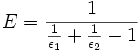
E = \frac{1}{\frac{1}{\epsilon_1} + \frac{1}{\epsilon_2} - 1}

Für praktische Anwendungen wird auch noch die Differenz der Potenzen der Temperaturen anders dargestellt:

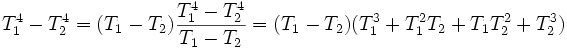
T_1^4 - T_2^4 = (T_1 - T_2) \frac{ T_1^4 - T_2^4}{ T_1 - T_2} = (T_1 - T_2) (T_1^3 + T_1^2 T_2 + T_1 T_2^2 + T_2^3)

Und für praktische Zwecke wird eine Temperatur Tm definiert:

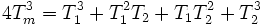
4 T_m^3 = T_1^3 + T_1^2 T_2 + T_1 T_2^2 + T_2^3

Die Temperatur Tm liegt zwischen T1 und T2. Wenn die beiden Temperaturen keinen großen Unterschied haben, reicht es oft für Tm den Mittelwert beider Temperaturen zu nehmen oder sogar T1 oder T2.

Geschichte

Stefan hat das Stefan-Boltzmann-Gesetz auf Grund des Strahlungsaustauschs entdeckt. In seiner Arbeit von 1879 "Über die Beziehung zwischen der Wärmestrahlung und der Temperatur" (Sitzungsberichte der mathematisch-naturwissenschaftlichen Classe der kaiserlichen Akademie der Wissenschaften - Wien 1879) hat er auf Seite 414 die Gleichung für den Strahlungsaustausch (siehe oben) verwendet, die seine Versuchsergebnisse am Besten beschrieben hat. Da er natürlich noch nicht die heutige Meßtechnik hatte, hat er der Wärmestrom über die Abkühlgeschwindigkeit, d.h. über die zeitliche Änderung der Temperatur T1 bestimmt.

Literatur

Vortmeyer, D.: VDI-Wärmeatlas - Berechnungsblätter für den Wärmeübergang. 6. Auflage. Springer-Verlag 1991
DIN EN ISO 9288: Wärmeübertragung durch Strahlung
DIN EN ISO 6946: Wärmedurchlasswiderstand und Wärmedurchgangskoeffizient - Berechnungsverfahren

Von "http://de.wikipedia.org/wiki/Strahlungsaustausch"